Forward Structure

In smash, a forward/direct spatially distributed model is obtained by chaining differentiable hydrological-hydraulic operators via simulated fluxes:

• (optional) a descriptors-to-parameters mapping \(\phi\), either for parameters imposing spatial constraints and/or regional mapping between physical descriptors and model conceptual parameters, see mapping section.

• (optional) a snow operator \(\mathcal{M}_{snw}\) generating a melt flux \(m_{lt}\), which is then summed with the precipitation flux to feed the hydrological operator \(\mathcal{M}_{rr}\).

• A hydrological production operator \(\mathcal{M}_{rr}\) generating an elementary discharge \(q_t\), which feeds the routing operator.

• A routing operator \(\mathcal{M}_{hy}\) simulating the propagation of discharge \(Q\).

The operators’ chaining principle is presented in section forward and inverse problems statement (cf. Eq. (2)), and the chaining fluxes are explicated in the diagram below. The forward model obtained reads \(\mathcal{M}=\mathcal{M}_{hy}\left(\,.\,,\mathcal{M}_{rr}\left(\,.\,,\mathcal{M}_{snw}\left(.\right)\right)\right)\).

This section describes the various operators available in smash with mathematical/numerical expressions, input data \(\left[\boldsymbol{I},\boldsymbol{D}\right](x,t)\), tunable conceptual parameters \(\boldsymbol{\theta}(x,t)\), and simulated state and fluxes \(\boldsymbol{U}(x,t)=\left[Q,\boldsymbol{h},\boldsymbol{q}\right](x,t)\).

These operators are written below for a given pixel \(x\) of the 2D spatial domain \(\Omega\) and for a time \(t\) in the simulation window \(\left]0,T\right]\).

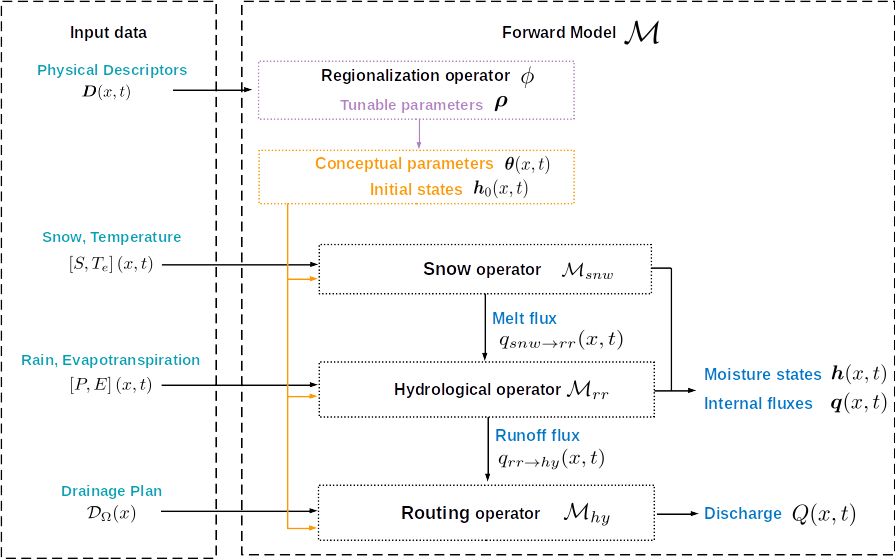
Diagram of input data, hydrological-hydraulic operators, simulated quantities of a forward model \(\mathcal{M}=\mathcal{M}_{hy}\left(\,.\,,\mathcal{M}_{rr}\left(\,.\,,\mathcal{M}_{snw}\left(.\right)\right)\right)\) (cf. Eq. (2)); recall the composition principle is explained in section forward and inverse problems statement.

Snow operator \(\mathcal{M}_{snw}\)

zero (Zero Snow)

This snow operator simply means that there is no snow operator.

\[m_{lt}(x, t) = 0\]

with \(m_{lt}\) the melt flux.

ssn (Simple Snow)

This snow operator is a simple degree-day snow operator. It can be expressed as follows:

\[m_{lt}(x, t) = f\left(\left[S, T_e\right](x, t), k_{mlt}(x), h_s(x, t)\right)\]

with \(m_{lt}\) the melt flux, \(S\) the snow, \(T_e\) the temperature, \(k_{mlt}\) the melt coefficient and \(h_s\) the state of the snow reservoir.

Note

Linking with the forward problem equation (1)

• Internal fluxes: \(\{m_{lt}\}\in\boldsymbol{q}\)

• Atmospheric forcings: \(\{S, T_e\}\in\boldsymbol{\mathcal{I}}\)

• Parameters: \(\{k_{mlt}\}\in\boldsymbol{\theta}\)

• States: \(\{h_s\}\in\boldsymbol{h}\)

The function \(f\) is resolved numerically as follows:

• Update the snow reservoir state \(h_s\) for \(t^* \in \left] t-1 , t\right[\)

\[h_s(x, t^*) = h_s(x, t-1) + S(x, t)\]

• Compute the melt flux \(m_{lt}\)

\begin{eqnarray} m_{lt}(x, t) = \begin{cases} 0 &\text{if} \; T_e(x, t) \leq 0 \\ \min\left(h_s(x, t^*), k_{mlt}(x)\times T_e(x, t)\right) &\text{otherwise} \end{cases} \end{eqnarray}

• Update the snow reservoir state \(h_s\)

\[h_s(x, t) = h_s(x, t^*) - m_{lt}(x, t)\]

Hydrological operator \(\mathcal{M}_{rr}\)

Hydrological processes can be described at pixel scale in smash with one of the available hydrological operators adapted from state-of-the-art lumped or distributed models.

Génie Rural with 4 parameters (gr4)

This hydrological operator is derived from the GR4 model [Perrin et al., 2003].

Hint

Helpful links about GR:

• Brief history of GR models

• Scientific papers

• GR models in a R package

Diagram of the gr4 like hydrological operator

It can be expressed as follows:

\[q_{t}(x, t) = f\left(\left[P, E\right](x, t), m_{lt}(x, t), \left[c_i, c_p, c_t, k_{exc}\right](x), \left[h_i, h_p, h_t\right](x, t)\right)\]

with \(q_{t}\) the elemental discharge, \(P\) the precipitation, \(E\) the potential evapotranspiration, \(m_{lt}\) the melt flux from the snow operator, \(c_i\) the maximum capacity of the interception reservoir, \(c_p\) the maximum capacity of the production reservoir, \(c_t\) the maximum capacity of the transfer reservoir, \(k_{exc}\) the exchange coefficient, \(h_i\) the state of the interception reservoir, \(h_p\) the state of the production reservoir and \(h_t\) the state of the transfer reservoir.

Note

Linking with the forward problem equation (1)

• Internal fluxes: \(\{q_{t}, m_{lt}\}\in\boldsymbol{q}\)

• Atmospheric forcings: \(\{P, E\}\in\boldsymbol{\mathcal{I}}\)

• Parameters: \(\{c_i, c_p, c_t, k_{exc}\}\in\boldsymbol{\theta}\)

• Normalized states: \(\{\tilde{h_i}, \tilde{h_p}, \tilde{h_t}\}\), where \(\tilde{h_i} = \frac{h_i}{c_i}\), \(\tilde{h_p} = \frac{h_p}{c_p}\), and \(\tilde{h_t} = \frac{h_t}{c_t}\), with states \(\{h_i, h_p, h_t\} \in \boldsymbol{h}\)

The function \(f\) is resolved numerically as follows:

Interception

• Compute interception evapotranspiration \(e_i\)

\[e_i(x, t) = \min(E(x, t), P(x, t) + m_{lt}(x, t) + \tilde{h_i}(x, t - 1)\times c_i(x))\]

• Compute the neutralized precipitation \(p_n\) and evapotranspiration \(e_n\)

\begin{eqnarray} &p_n(x, t)& &=& &\max \left(0, \; P(x, t) + m_{lt}(x, t) - c_i(x) \times (1 - \tilde{h_i}(x, t - 1)) - e_i(x, t) \right)\\ &e_n(x, t)& &=& &E(x, t) - e_i(x, t) \end{eqnarray}

• Update the interception reservoir state \(\tilde{h_i}\)

\[\tilde{h_i}(x, t) = \tilde{h_i}(x, t - 1) + \frac{P(x, t) + m_{lt}(x, t) + e_i(x, t) - p_n(x, t)}{c_i(x)}\]

Production

• Compute the production infiltrating precipitation \(p_s\) and evapotranspiration \(e_s\)

\begin{eqnarray} &p_s(x, t)& &=& &c_p(x) (1 - \tilde{h_p}(x, t - 1)^2) \frac{\tanh\left(\frac{p_n(x, t)}{c_p(x)}\right)}{1 + \tilde{h_p}(x, t - 1) \tanh\left(\frac{p_n(x, t)}{c_p(x)}\right)}\\ &e_s(x, t)& &=& &\tilde{h_p}(x, t - 1) c_p(x) (2 - \tilde{h_p}(x, t - 1)) \frac{\tanh\left(\frac{e_n(x, t)}{c_p(x)}\right)}{1 + (1 - \tilde{h_p}(x, t - 1)) \tanh\left(\frac{e_n(x, t)}{c_p(x)}\right)} \end{eqnarray}

• Update the normalized production reservoir state \(\tilde{h_p}\)

\[\tilde{h_p}(x, t^*) = \tilde{h_p}(x, t - 1) + \frac{p_s(x, t) - e_s(x, t)}{c_p(x)}\]

• Compute the production runoff \(p_r\)

\begin{eqnarray} p_r(x, t) = \begin{cases} 0 &\text{if} \; p_n(x, t) \leq 0 \\ p_n(x, t) - p_s(x, t) &\text{otherwise} \end{cases} \end{eqnarray}

• Compute the production percolation \(p_{erc}\)

\[p_{erc}(x, t) = \tilde{h_p}(x, t^*) c_p(x) \left(1 - \left(1 + \left(\frac{4}{9}\tilde{h_p}(x, t^*)\right)^4\right)^{-1/4}\right)\]

• Update the normalized production reservoir state \(\tilde{h_p}\)

\[\tilde{h_p}(x, t) = \tilde{h_p}(x, t^*) - \frac{p_{erc}(x, t)}{c_p(x)}\]

Exchange

• Compute the exchange flux \(l_{exc}\)

\[l_{exc}(x, t) = k_{exc}(x) \tilde{h_t}(x, t - 1)^{7/2}\]

Transfer

• Split the production runoff and percolation \(p_r+p_{erc}\) into two branches (transfer and direct), \(p_{rr}\) and \(p_{rd}\)

\begin{eqnarray} &p_{rr}(x, t)& &=& &0.9(p_r(x, t) + p_{erc}(x, t)) + l_{exc}(x, t)\\ &p_{rd}(x, t)& &=& &0.1(p_r(x, t) + p_{erc}(x, t)) \end{eqnarray}

• Update the normalized transfer reservoir state \(\tilde{h_t}\)

\[\tilde{h_t}(x, t^*) = \max\left(0, \tilde{h_t}(x, t - 1) + \frac{p_{rr}(x, t)}{c_t(x)}\right)\]

• Compute the transfer branch elemental discharge \(q_r\)

\begin{eqnarray} q_r(x, t) = \tilde{h_t}(x, t^*)c_t(x) - \left(\left(\tilde{h_t}(x, t^*)c_t(x)\right)^{-4} + c_t(x)^{-4}\right)^{-1/4} \end{eqnarray}

• Update the normalized transfer reservoir state \(\tilde{h_t}\)

\[\tilde{h_t}(x, t) = \tilde{h_t}(x, t^*) - \frac{q_r(x, t)}{c_t(x)}\]

• Compute the direct branch elemental discharge \(q_d\)

\[q_d(x, t) = \max(0, p_{rd}(x, t) + l_{exc}(x, t))\]

• Compute the elemental discharge \(q_t\)

\[q_t(x, t) = q_r(x, t) + q_d(x, t)\]

Génie Rural with 5 parameters (gr5)

This hydrological operator is derived from the GR5 model [Le Moine, 2008]. It consists in a gr4 like model structure (see diagram above) with a modified exchange flux with two parameters to account for seasonal variations.

Hint

Helpful links about GR:

• Brief history of GR models

• Scientific papers

• GR models in a R package

Diagram of the gr5 like hydrological operator

It can be expressed as follows:

\[q_{t}(x, t) = f\left(\left[P, E\right](x, t), m_{lt}(x, t), \left[c_i, c_p, c_t, k_{exc}, a_{exc}\right](x), \left[h_i, h_p, h_t\right](x, t)\right)\]

with \(q_{t}\) the elemental discharge, \(P\) the precipitation, \(E\) the potential evapotranspiration, \(m_{lt}\) the melt flux from the snow operator, \(c_i\) the maximum capacity of the interception reservoir, \(c_p\) the maximum capacity of the production reservoir, \(c_t\) the maximum capacity of the transfer reservoir, \(k_{exc}\) the exchange coefficient, \(a_{exc}\) the exchange threshold, \(h_i\) the state of the interception reservoir, \(h_p\) the state of the production reservoir and \(h_t\) the state of the transfer reservoir.

Note

Linking with the forward problem equation (1)

• Internal fluxes: \(\{q_{t}, m_{lt}\}\in\boldsymbol{q}\)

• Atmospheric forcings: \(\{P, E\}\in\boldsymbol{\mathcal{I}}\)

• Parameters: \(\{c_i, c_p, c_t, k_{exc}, a_{exc}\}\in\boldsymbol{\theta}\)

• Normalized states: \(\{\tilde{h_i}, \tilde{h_p}, \tilde{h_t}\}\), where \(\tilde{h_i} = \frac{h_i}{c_i}\), \(\tilde{h_p} = \frac{h_p}{c_p}\), and \(\tilde{h_t} = \frac{h_t}{c_t}\), with states \(\{h_i, h_p, h_t\} \in \boldsymbol{h}\)

The function \(f\) is resolved numerically as follows:

Interception

Same as gr4 interception, see GR4 Interception.

Production

Same as gr4 production, see GR4 Production.

Exchange

• Compute the exchange flux \(l_{exc}\)

\[l_{exc}(x, t) = k_{exc}(x) \left(\tilde{h_t}(x, t - 1) - a_{exc}(x)\right)\]

Transfer

Same as gr4 transfer, see GR4 Transfer.

Génie Rural with 6 parameters (gr6)

This hydrological module is derived from the GR6 model [Michel et al., 2003, Pushpalatha et al., 2011].

Hint

Helpful links about GR:

• Brief history of GR models

• Scientific papers

• GR models in a R package

Diagram of the gr6 like hydrological operator

It can be expressed as follows:

\[q_{t}(x, t) = f\left(\left[P, E\right](x, t), m_{lt}(x, t), \left[c_i, c_p, c_t, b_e, k_{exc}, a_{exc}\right](x), \left[h_i, h_p, h_t, h_e\right](x, t)\right)\]

with \(q_{t}\) the elemental discharge, \(P\) the precipitation, \(E\) the potential evapotranspiration, \(m_{lt}\) the melt flux from the snow module, \(c_i\) the maximum capacity of the interception reservoir, \(c_p\) the maximum capacity of the production reservoir, \(c_t\) the maximum capacity of the transfer reservoir, \(b_e\) controls the slope of the recession, \(k_{exc}\) the exchange coefficient, \(a_{exc}\) the exchange threshold, \(h_i\) the state of the interception reservoir, \(h_p\) the state of the production reservoir and \(h_t\) the state of the transfer reservoir, \(h_e\) the state of the exponential reservoir.

Note

Linking with the forward problem equation (1)

• Internal fluxes: \(\{q_{t}, m_{lt}\}\in\boldsymbol{q}\)

• Atmospheric forcings: \(\{P, E\}\in\boldsymbol{\mathcal{I}}\)

• Parameters: \(\{c_i, c_p, c_t, b_e, k_{exc}, a_{exc}\}\in\boldsymbol{\theta}\)

• States: \(\{h_e\}\in\boldsymbol{h}\)

• Normalized states: \(\{\tilde{h_i}, \tilde{h_p}, \tilde{h_t}\}\), where \(\tilde{h_i} = \frac{h_i}{c_i}\), \(\tilde{h_p} = \frac{h_p}{c_p}\), and \(\tilde{h_t} = \frac{h_t}{c_t}\), with states \(\{h_i, h_p, h_t\} \in \boldsymbol{h}\)

The function \(f\) is resolved numerically as follows:

Interception

Same as gr4 interception, see GR4 Interception.

Production

Same as gr4 production, see GR4 Production.

Exchange

Same as gr5 exchange, see GR5 Exchange.

Transfer

• Split the production runoff and percolation \(p_r+p_{erc}\) into three branches (transfer, exponential and direct), \(p_{rr}\), \(p_{re}\) and \(p_{rd}\)

\begin{eqnarray} &p_{rr}(x, t)& &=& &0.6 \times 0.9(p_r(x, t) + p_{erc}(x, t)) + l_{exc}(x, t)\\ &p_{re}(x, t)& &=& &0.4 \times 0.9(p_r(x, t) + p_{erc}(x, t)) + l_{exc}(x, t)\\ &p_{rd}(x, t)& &=& &0.1(p_r(x, t) + p_{erc}(x, t)) \end{eqnarray}

• Update the normalized transfer reservoir state \(\tilde{h_t}\)

\[\tilde{h_t}(x, t^*) = \max\left(0, \tilde{h_t}(x, t - 1) + \frac{p_{rr}(x, t)}{c_t(x)}\right)\]

• Compute the transfer branch elemental discharge \(q_r\)

\begin{eqnarray} q_r(x, t) = \tilde{h_t}(x, t^*)c_t(x) - \left(\left(\tilde{h_t}(x, t^*)c_t(x)\right)^{-4} + c_t(x)^{-4}\right)^{-1/4} \end{eqnarray}

• Update the normalized transfer reservoir state \(\tilde{h_t}\)

\[\tilde{h_t}(x, t) = \tilde{h_t}(x, t^*) - \frac{q_r(x, t)}{c_t(x)}\]

• Update the exponential state \(h_e\)

\[h_e(x, t^*) = h_e(x, t - 1) + p_{re}\]

• Compute the exponential branch elemental discharge \(q_{e}\)

\begin{eqnarray} q_{e}(x, t) = \begin{cases} b_e(x) \ln \left( 1 + \exp \left( \frac{h_e(x, t^*)}{b_e(x)} \right) \right) &\text{if} \; -7 \lt \frac{h_e(x, t^*)}{b_e(x)} \lt 7 \\ b_e(x) * \exp \left( \frac{h_e(x, t^*)}{b_e(x)} \right) &\text{if} \; \frac{h_e(x, t^*)}{b_e(x)} \lt -7 \\ h_e(x, t^*) + \frac{ b_e(x) }{ \exp \left( \frac{h_e(x, t^*)}{b_e(x)} \right) } \; &\text{otherwise}. \end{cases} \end{eqnarray}

• Update the exponential reservoir state \(h_e\)

\[h_e(x, t) = h_e(x, t^*) - q_{e}\]

• Compute the direct branch elemental discharge \(q_d\)

\[q_d(x, t) = \max(0, p_{rd}(x, t) + l_{exc}(x, t))\]

• Compute the elemental discharge \(q_t\)

\[q_t(x, t) = q_r(x, t) + q_{e}(x, t) + q_d(x, t)\]

Génie Rural C (grc)

This hydrological operator is derived from the GR models. It consists in a gr4 like model structure with a second transfer reservoir.

Diagram of the grc hydrological operator

It can be expressed as follows:

\[q_{t}(x, t) = f\left(\left[P, E\right](x, t), m_{lt}(x, t), \left[c_i, c_p, c_t, c_l, k_{exc}\right](x), \left[h_i, h_p, h_t, h_l\right](x, t)\right)\]

with \(q_{t}\) the elemental discharge, \(P\) the precipitation, \(E\) the potential evapotranspiration, \(m_{lt}\) the melt flux from the snow operator, \(c_i\) the maximum capacity of the interception reservoir, \(c_p\) the maximum capacity of the production reservoir, \(c_t\) the maximum capacity of the transfer reservoir, \(c_l\) the maximum capacity of the [slow-]transfer reservoir, \(k_{exc}\) the exchange coefficient, \(h_i\) the state of the interception reservoir, \(h_p\) the state of the production reservoir, \(h_t\) the state of the first transfer reservoir and \(h_l\) the state of the second transfer reservoir.

Note

Linking with the forward problem equation (1)

• Internal fluxes, \(\{q_{t}, m_{lt}\}\in\boldsymbol{q}\)

• Atmospheric forcings, \(\{P, E\}\in\boldsymbol{\mathcal{I}}\)

• Parameters, \(\{c_i, c_p, c_t, c_l, k_{exc}\}\in\boldsymbol{\theta}\)

• Normalized states: \(\{\tilde{h_i}, \tilde{h_p}, \tilde{h_t}, \tilde{h_l}\}\), where \(\tilde{h_i} = \frac{h_i}{c_i}\), \(\tilde{h_p} = \frac{h_p}{c_p}\), \(\tilde{h_t} = \frac{h_t}{c_t}\), and \(\tilde{h_l} = \frac{h_l}{c_l}\), with states \(\{h_i, h_p, h_t, h_l\} \in \boldsymbol{h}\)

The function \(f\) is resolved numerically as follows:

Interception

Same as gr4 interception, see GR4 Interception.

Production

Same as gr4 production, see GR4 Production.

Exchange

Same as gr4 exchange, see GR4 Exchange.

Transfer

• Split the production runoff and percolation \(p_r+p_{erc}\) into three branches (first transfer, second transfer and direct), \(p_{rr}\), \(p_{rl}\) and \(p_{rd}\)

\begin{eqnarray} &p_{rr}(x, t)& &=& &0.6 \times 0.9(p_r(x, t) + p_{erc}(x, t)) + l_{exc}(x, t)\\ &p_{rl}(x, t)& &=& &0.4 \times 0.9(p_r(x, t) + p_{erc}(x, t)) \\ &p_{rd}(x, t)& &=& &0.1(p_r(x, t) + p_{erc}(x, t)) \end{eqnarray}

• Update the normalized transfer reservoir states \(\tilde{h_t}\) and \(\tilde{h_l}\)

\[\tilde{h_t}(x, t^*) = \max\left(0, \tilde{h_t}(x, t - 1) + \frac{p_{rr}(x, t)}{c_t(x)}\right)\]

\[\tilde{h_l}(x, t^*) = \max\left(0, \tilde{h_l}(x, t - 1) + \frac{p_{rl}(x, t)}{c_l(x)}\right)\]

• Compute the transfer branch elemental discharges \(q_r\) and \(q_l\)

\begin{eqnarray} &q_r(x, t)& &=& &\tilde{h_t}(x, t^*)c_t(x) - \left(\left(\tilde{h_t}(x, t^*)c_t(x)\right)^{-4} + c_t(x)^{-4}\right)^{-1/4}\\ &q_l(x, t)& &=& &\tilde{h_l}(x, t^*)c_l(x) - \left(\left(\tilde{h_l}(x, t^*)c_l(x)\right)^{-4} + c_l(x)^{-4}\right)^{-1/4} \end{eqnarray}

• Update the normalized transfer reservoir states \(\tilde{h_t}\) and \(\tilde{h_l}\)

\[\tilde{h_t}(x, t) = \tilde{h_t}(x, t^*) - \frac{q_r(x, t)}{c_t(x)}\]

\[\tilde{h_l}(x, t) = \tilde{h_l}(x, t^*) - \frac{q_l(x, t)}{c_l(x)}\]

• Compute the direct branch elemental discharge \(q_d\)

\[q_d(x, t) = \max(0, p_{rd}(x, t) + l_{exc}(x, t))\]

• Compute the elemental discharge \(q_t\)

\[q_t(x, t) = q_r(x, t) + q_l(x, t) + q_d(x, t)\]

Génie Rural Distribué (grd)

This hydrological operator is derived from the GR models and is a simplified structure used in Jay-Allemand et al. [2020].

Diagram of the grd hydrological operator, a simplified GR like

It can be expressed as follows:

\[q_{t}(x, t) = f\left(\left[P, E\right](x, t), m_{lt}(x, t), \left[c_p, c_t\right](x), \left[h_p, h_t\right](x, t)\right)\]

with \(q_{t}\) the elemental discharge, \(P\) the precipitation, \(E\) the potential evapotranspiration, \(m_{lt}\) the melt flux from the snow operator, \(c_p\) the maximum capacity of the production reservoir, \(c_t\) the maximum capacity of the transfer reservoir, \(h_p\) the state of the production reservoir and \(h_t\) the state of the transfer reservoir.

Note

Linking with the forward problem equation (1)

• Internal fluxes: \(\{q_{t}, m_{lt}\}\in\boldsymbol{q}\)

• Atmospheric forcings: \(\{P, E\}\in\boldsymbol{\mathcal{I}}\)

• Parameters: \(\{c_p, c_t\}\in\boldsymbol{\theta}\)

• Normalized states: \(\{\tilde{h_p}, \tilde{h_t}\}\), where \(\tilde{h_p} = \frac{h_p}{c_p}\) and \(\tilde{h_t} = \frac{h_t}{c_t}\), with states \(\{h_p, h_t\} \in \boldsymbol{h}\)

The function \(f\) is resolved numerically as follows:

Interception

• Compute the interception evapotranspiration \(e_i\)

\[e_i(x, t) = \min(E(x, t), P(x, t) + m_{lt}(x, t))\]

• Compute the neutralized precipitation \(p_n\) and evapotranspiration \(e_n\)

\begin{eqnarray} &p_n(x, t)& &=& &\max \left(0, \; P(x, t) + m_{lt}(x, t) - e_i(x, t) \right)\\ &e_n(x, t)& &=& &E(x, t) - e_i(x, t) \end{eqnarray}

Production

Same as gr4 production, see GR4 Production.

Transfer

• Update the normalized transfer reservoir state \(\tilde{h_t}\)

\[\tilde{h_t}(x, t^*) = \max\left(0, \tilde{h_t}(x, t - 1) + \frac{p_{r}(x, t)}{c_t(x)}\right)\]

• Compute the transfer branch elemental discharge \(q_r\)

\begin{eqnarray} q_r(x, t) = \tilde{h_t}(x, t^*)c_t(x) - \left(\left(\tilde{h_t}(x, t^*)c_t(x)\right)^{-4} + c_t(x)^{-4}\right)^{-1/4} \end{eqnarray}

• Update the normalized transfer reservoir state \(\tilde{h_t}\)

\[\tilde{h_t}(x, t) = \tilde{h_t}(x, t^*) - \frac{q_r(x, t)}{c_t(x)}\]

• Compute the elemental discharge \(q_t\)

\[q_t(x, t) = q_r(x, t)\]

Génie Rural LoiEau (loieau)

This hydrological operator is derived from the GR model [Folton and Arnaud, 2020].

Hint

Helpful links about LoiEau:

• Database

Diagram of the loieau like hydrological operator

It can be expressed as follows:

\[q_{t}(x, t) = f\left(\left[P, E\right](x, t), m_{lt}(x, t), \left[c_a, c_c, k_b\right](x), \left[h_a, h_c\right](x, t)\right)\]

with \(q_{t}\) the elemental discharge, \(P\) the precipitation, \(E\) the potential evapotranspiration, \(m_{lt}\) the melt flux from the snow operator, \(c_a\) the maximum capacity of the production reservoir, \(c_c\) the maximum capacity of the transfer reservoir, \(k_b\) the transfer coefficient, \(h_a\) the state of the production reservoir and \(h_c\) the state of the transfer reservoir.

Note

Linking with the forward problem equation (1)

• Internal fluxes: \(\{q_{t}, m_{lt}\}\in\boldsymbol{q}\)

• Atmospheric forcings: \(\{P, E\}\in\boldsymbol{\mathcal{I}}\)

• Parameters: \(\{c_a, c_c, k_b\}\in\boldsymbol{\theta}\)

• Normalized states: \(\{\tilde{h_a}, \tilde{h_c}\}\), where \(\tilde{h_a} = \frac{h_a}{c_a}\) and \(\tilde{h_c} = \frac{h_c}{c_c}\), with states \(\{h_a, h_c\} \in \boldsymbol{h}\)

The function \(f\) is resolved numerically as follows:

Interception

Same as grd interception, see GRD Interception.

Production

Same as gr4 production, see GR4 Production.

Note

The parameter \(c_p\) is replaced by \(c_a\) and the state \(h_p\) by \(h_a\)

Transfer

• Split the production runoff and percolation \(p_r+p_{erc}\) into two branches (transfer and direct), \(p_{rr}\) and \(p_{rd}\)

\begin{eqnarray} &p_{rr}(x, t)& &=& &0.9(p_r(x, t) + p_{erc}(x, t))\\ &p_{rd}(x, t)& &=& &0.1(p_r(x, t) + p_{erc}(x, t)) \end{eqnarray}

• Update the normalized transfer reservoir state \(\tilde{h_c}\)

\[\tilde{h_c}(x, t^*) = \max\left(0, \tilde{h_c}(x, t - 1) + \frac{p_{rr}(x, t)}{c_c(x)}\right)\]

• Compute the transfer branch elemental discharge \(q_r\)

\begin{eqnarray} q_r(x, t) = \tilde{h_c}(x, t^*)c_c(x) - \left(\left(\tilde{h_c}(x, t^*)c_c(x)\right)^{-3} + c_c(x)^{-3}\right)^{-1/3} \end{eqnarray}

• Update the normalized transfer reservoir state \(\tilde{h_c}\)

\[\tilde{h_c}(x, t) = \tilde{h_c}(x, t^*) - \frac{q_r(x, t)}{c_c(x)}\]

• Compute the direct branch elemental discharge \(q_d\)

\[q_d(x, t) = \max(0, p_{rd}(x, t))\]

• Compute the elemental discharge \(q_t\)

\[q_t(x, t) = k_b(x)\left(q_r(x, t) + q_d(x, t)\right)\]

Génie Rural with rainfall intensity terms (gr4_ri, gr5_ri)

gr4_ri

This hydrological module is derived from the model introduced in Astagneau et al. [2022].

Diagram of the gr4_ri like hydrological operator

It can be expressed as follows:

\[q_{t}(x, t) = f\left(\left[P, E\right](x, t), m_{lt}(x, t), \left[c_i, c_p, c_t, \alpha_1, \alpha_2, k_{exc}\right](x), \left[h_i, h_p, h_t\right](x, t)\right)\]

with \(q_{t}\) the elemental discharge, \(P\) the precipitation, \(E\) the potential evapotranspiration, \(m_{lt}\) the melt flux from the snow operator, \(c_i\) the maximum capacity of the interception reservoir, \(c_p\) the maximum capacity of the production reservoir, \(c_t\) the maximum capacity of the transfer reservoir, \(k_{exc}\) the exchange coefficient, \(h_i\) the state of the interception reservoir, \(h_p\) the state of the production reservoir and \(h_t\) the state of the transfer reservoir, \(\alpha_1\) and \(\alpha_2\) parameters controling the rainfall intensity rate respectively in time unit per \(mm\) and in \(mm\) per time unit.

Note

Linking with the forward problem equation (1)

• Internal fluxes: \(\{q_{t}, m_{lt}\}\in\boldsymbol{q}\)

• Atmospheric forcings: \(\{P, E\}\in\boldsymbol{\mathcal{I}}\)

• Parameters: \(\{c_i, c_p, c_t, \alpha_1, \alpha_2, k_{exc}\}\in\boldsymbol{\theta}\)

• Normalized states: \(\{\tilde{h_i}, \tilde{h_p}, \tilde{h_t}\}\), where \(\tilde{h_i} = \frac{h_i}{c_i}\), \(\tilde{h_p} = \frac{h_p}{c_p}\), and \(\tilde{h_t} = \frac{h_t}{c_t}\), with states \(\{h_i, h_p, h_t\} \in \boldsymbol{h}\)

The function \(f\) is resolved numerically as follows:

Interception

Same as gr4 interception, see GR4 Interception.

Production

In the classical GR production reservoir formulation, the instantaneous production rate is the ratio between the state and the capacity of the reservoir, \(\eta = \tilde{h_p}^2\). The infiltration flux \(p_s\) is obtained by temporal integration as follows:

\begin{eqnarray} &p_s = \int_{t-\Delta t}^{t} (1 - \eta) dt \\ \end{eqnarray}

Assuming the neutralized rainfall \(p_n\) constant over the current time step and thanks to analytically integrable function, the infiltration flux into the production reservoir is obtained:

\begin{eqnarray} &p_s = & c_p \tanh\left(\frac{p_n}{c_p}\right) \frac{1 - \tilde{h_p}^2}{1 + \tilde{h_p} \tanh\left( \frac{p_n}{c_p} \right)} \\ \end{eqnarray}

To improve runoff production by a GR reservoir, even with low production level in dry condition, in the case of high rainfall intensity, in Astagneau et al. [2022] they suggest a modification of the infiltration rate \(p_s\) depending on rainfall intensity \(p_n\). Indeed, let’s consider the rainfall intensity coefficient \(\gamma\), function of weighted rainfall intensity.

\begin{eqnarray} & \gamma = & 1 - \exp(-p_n \times \alpha_1) \\ \end{eqnarray}

with \(\alpha_1\) in time unit per \(mm\).

The expression of the instantaneous production rate changes as follows

\begin{eqnarray} & \eta = & \left( 1 - \gamma \right) \tilde{h_p}^2 + \gamma \\ \end{eqnarray}

Thus the infiltration rate becomes

\begin{eqnarray} &p_s& &=& &\int_{t-\Delta t}^{t} (1 - \eta) dt\\ && &=& &\int_{t-\Delta t}^{t} \left(1 - (1-\gamma) \tilde{h_p}^2 \right) dt - \int_{t-\Delta t}^{t} \gamma dt\\ && &=& &\left[ \frac{ c_p }{ \sqrt{1-\gamma} } \tanh \left( \frac{\sqrt{1-\gamma}}{c_p} \tilde{h_p} \right) \right]_{t-\Delta t}^t - \gamma \Delta t \end{eqnarray}

We denote \(\lambda = \sqrt{1 - \gamma}\), then

\begin{eqnarray} \tanh \left( \lambda \tilde{h_p} + \frac{p_n}{c_p} \right) - \tanh\left( \lambda \tilde{h_p} \right) &=& \tanh \left( \lambda \frac{p_n}{c_p} \right) \left(1 - \tanh \left( \lambda \tilde{h_p} + \frac{p_n}{c_p} \right) \tanh \left( \lambda \tilde{h_p} \right) \right) \\ &=& \tanh \left( \lambda \frac{p_n}{c_p} \right) \left(1 - \frac{ \tanh \left( \lambda \tilde{h_p} \right) + \tanh \left( \lambda \frac{p_n}{c_p} \right) } { 1 + \tanh \left( \lambda \tilde{h_p} \right) \tanh \left( \lambda \frac{p_n}{c_p} \right) } \tanh \left( \lambda \tilde{h_p} \right) \right) \\ &\sim& \tanh \left( \lambda \frac{p_n}{c_p} \right) \left(1 - \frac{ \lambda \tilde{h_p} + \tanh \left( \lambda \frac{p_n}{c_p} \right) } { 1 + \lambda \tilde{h_p} \tanh \left( \lambda \frac{p_n}{c_p} \right) } \lambda \tilde{h_p} \right) \\ &=& \tanh \left( \lambda \frac{p_n}{c_p} \right) \frac{1 - \left( \lambda \tilde{h_p} \right)^2}{1 + \lambda \tilde{h_p} \tanh \left( \lambda \frac{p_n}{c_p} \right)} \end{eqnarray}

Thus

\begin{eqnarray} p_s &=& \frac{c_p}{\lambda} \tanh \left( \lambda \frac{p_n}{c_p} \right) \frac{1 - \left( \lambda \tilde{h_p} \right)^2}{1 + \lambda \tilde{h_p} \tanh \left( \lambda \frac{p_n}{c_p} \right)} - \gamma \Delta t \end{eqnarray}

Note

Note that if \(\alpha_1 = 0\), we return to the general writing of the instantaneous production rate.

Exchange

Same as gr4 exchange, see GR4 Exchange.

Transfer

In context of high rainfall intensities triggering flash flood responses, it is crucial to account for fast dynamics related to surface/hypodermic runoff and slower responses due to delayed/deeper flows (e.g. Douinot et al. [2018]). Following Astagneau et al. [2022] for a lumped GR model, we introduce at pixel scale in smash a function to modify the partitioning between fast and slower transfert branches depending on rainfall intensity of the current time step only (small pixel size):

\begin{eqnarray} &p_{rr}& =& (1 - spl)(p_r + p_{erc}) + l_{exc}\\ &p_{rd}& =& spl(p_r + p_{erc}) \\ &spl& =& 0.9 \tanh(\alpha_2 p_n)^2 + 0.1 \end{eqnarray}

with \(\alpha_2\) in \(mm\) per time unit.

Note

If \(\alpha_2 = 0\), we return to the gr-4 writing of the transfer. If \(\alpha_2 = \alpha_1 = 0\), it is equivalent to gr-4 structure.

gr5_ri

This hydrological module is derived from the model introduced in Astagneau et al. [2022].

Diagram of the gr5_ri like hydrological operator

It can be expressed as follows:

\[q_{t}(x, t) = f\left(\left[P, E\right](x, t), m_{lt}(x, t), \left[c_i, c_p, c_t, \alpha_1, \alpha_2, k_{exc}, a_{exc}\right](x), \left[h_i, h_p, h_t\right](x, t)\right)\]

with \(q_{t}\) the elemental discharge, \(P\) the precipitation, \(E\) the potential evapotranspiration, \(m_{lt}\) the melt flux from the snow operator, \(c_i\) the maximum capacity of the interception reservoir, \(c_p\) the maximum capacity of the production reservoir, \(c_t\) the maximum capacity of the transfer reservoir, \(k_{exc}\) the exchange coefficient, \(a_{exc}\) the exchange threshold, \(h_i\) the state of the interception reservoir, \(h_p\) the state of the production reservoir and \(h_t\) the state of the transfer reservoir, \(\alpha_1\) and \(\alpha_2\) parameters controling the rainfall intensity rate respectively in time unit per \(mm\) and in \(mm\) per time unit.

Note

Linking with the forward problem equation (1)

• Internal fluxes: \(\{q_{t}, m_{lt}\}\in\boldsymbol{q}\)

• Atmospheric forcings: \(\{P, E\}\in\boldsymbol{\mathcal{I}}\)

• Parameters: \(\{c_i, c_p, c_t, \alpha_1, \alpha_2, k_{exc}, a_{exc}\}\in\boldsymbol{\theta}\)

• Normalized states: \(\{\tilde{h_i}, \tilde{h_p}, \tilde{h_t}\}\), where \(\tilde{h_i} = \frac{h_i}{c_i}\), \(\tilde{h_p} = \frac{h_p}{c_p}\), and \(\tilde{h_t} = \frac{h_t}{c_t}\), with states \(\{h_i, h_p, h_t\} \in \boldsymbol{h}\)

The function \(f\) is resolved numerically as follows:

Interception

Same as gr4 interception, see GR4 Interception.

Production

Same as gr4_ri production, see GR4 Production.

Exchange

Same as gr5 exchange, see GR5 Exchange.

Transfer

Same as gr4_ri transfer, see GR4 Transfer.

Hybrid GR for flux correction (gr4_mlp, gr5_mlp, gr6_mlp, grc_mlp, grd_mlp, loieau_mlp)

These hydrological models are GR-like models embedded within a multilayer perceptron (MLP) to correct internal water fluxes. Such a neural network is referred to as a process-parameterization neural network. This process-parameterization neural network takes as inputs the neutralized precipitation, the neutralized potential evapotranspiration, and the model states from the previous time step, and produces the corrections of internal water fluxes as outputs:

\[\boldsymbol{f}_{q}(x,t) = \phi\left(\boldsymbol{I}_n(x,t),\boldsymbol{h}(x,t-1);\boldsymbol{\rho}\right)\]

where \(\boldsymbol{f}_{q}\) is the vector of flux corrections, \(\boldsymbol{I}_n\) is the neutralized atmospheric forcings, \(\boldsymbol{h}\) is the vector of model states, and \(\boldsymbol{\rho}\) is the parameters of the process-parameterization neural network \(\phi\).

Note

The output layer of this neural network uses a TanH activation function to map the hydrological flux corrections to the range \(]-1, 1[\).

gr4_mlp

This hydrological module is principally based on the gr4 operators, with the integration of a neural network for correcting internal water fluxes as follows:

Interception

Same as gr4 interception, see GR4 Interception.

Process-parameterization neural network

\[[f_p, f_e, f_c, f_l](x,t) = \phi\left([p_n, e_n](x,t), [\tilde{h_p}, \tilde{h_t}](x,t-1);\boldsymbol{\rho}\right)\]

where \(p_n, e_n\) are the neutralized precipitation and potential evapotranspiration obtained from interception; \(\tilde{h_p}, \tilde{h_t}\) are the normalized states of the production and transfer reservoirs; \(f_p, f_e, f_c, f_l\) are the corrections applied to internal fluxes as follows.

Production

Similar to gr4 production, but the equations for computing infiltrating precipitation \(p_s\) and evapotranspiration \(e_s\) are updated to integrate flux corrections

\begin{eqnarray} &p_s(x, t)& & := & &\min\left(p_n(x, t), (1 + f_p) p_s(x, t)\right) \\ &e_s(x, t)& & := & &\min\left(e_n(x, t), (1 + f_e) e_s(x, t)\right) \end{eqnarray}

Exchange

Compute the refined exchange flux

\[l_{exc}(x, t) = (1 + f_l) k_{exc}(x) \tilde{h_t}(x, t - 1)^{7/2}\]

Transfer

Same as gr4 transfer except the equations of splitting the production runoff and percolation \(p_r+p_{erc}\)

\begin{eqnarray} &p_{rr}(x, t)& &=& &(0.9 - 0.9 f_c^2)(p_r(x, t) + p_{erc}(x, t)) + l_{exc}(x, t)\\ &p_{rd}(x, t)& &=& &(0.1 + 0.9 f_c^2)(p_r(x, t) + p_{erc}(x, t)) \end{eqnarray}

gr5_mlp

This hydrological module is principally based on the gr5 operators, with the integration of a neural network for correcting internal water fluxes as follows:

Interception

Same as gr4 interception.

Process-parameterization neural network

Same as gr4_mlp process-parameterization neural network.

Production

Same as gr4_mlp production.

Exchange

Compute the refined exchange flux

\[l_{exc}(x, t) = (1 + f_l) k_{exc}(x) \left(\tilde{h_t}(x, t - 1) - a_{exc}(x)\right)\]

Transfer

Same as gr4_mlp transfer.

gr6_mlp

This hydrological module is principally based on the gr6 operators, with the integration of a neural network for correcting internal water fluxes as follows:

Interception

Same as gr4 interception.

Process-parameterization neural network

\[[f_p, f_e, f_{c1}, f_{c2}, f_l](x,t) = \phi\left([p_n, e_n](x,t), [\tilde{h_p}, \tilde{h_t}, \tilde{h_e}](x,t-1);\boldsymbol{\rho}\right)\]

where \(p_n, e_n\) are the neutralized precipitation and potential evapotranspiration obtained from interception; \(\tilde{h_p}, \tilde{h_t}\) are the normalized states of the production and transfer reservoirs; \(h_e\) is the state of the exponential reservoir; \(f_p, f_e, f_{c1}, f_{c2}, f_l\) are the corrections applied to internal fluxes as follows.

Production

Same as gr4_mlp production.

Exchange

Same as gr5_mlp exchange.

Transfer

Same as gr6 transfer except the equations of splitting the production runoff and percolation \(p_r+p_{erc}\)

\begin{eqnarray} &p_{rr}(x, t)& &=& &(0.6 - 0.4 f_{c2}) (0.9 - 0.9 f_{c1}^2) (p_r(x, t) + p_{erc}(x, t)) + l_{exc}(x, t)\\ &p_{re}(x, t)& &=& &(0.4 + 0.4 f_{c2}) (0.9 - 0.9 f_{c1}^2) (p_r(x, t) + p_{erc}(x, t)) + l_{exc}(x, t)\\ &p_{rd}(x, t)& &=& &(0.1 + 0.9 f_{c1}^2) (p_r(x, t) + p_{erc}(x, t)) \end{eqnarray}

grc_mlp

This hydrological module is principally based on the grc operators, with the integration of a neural network for correcting internal water fluxes as follows:

Interception

Same as gr4 interception.

Process-parameterization neural network

\[[f_p, f_e, f_{c1}, f_{c2}, f_l](x,t) = \phi\left([p_n, e_n](x,t), [\tilde{h_p}, \tilde{h_t}, \tilde{h_l}](x,t-1);\boldsymbol{\rho}\right)\]

where \(p_n, e_n\) are the neutralized precipitation and potential evapotranspiration obtained from interception; \(\tilde{h_p}, \tilde{h_t}, \tilde{h_l}\) are the normalized states of the production, first transfer, and second transfer reservoirs; \(f_p, f_e, f_{c1}, f_{c2}, f_l\) are the corrections applied to internal fluxes as follows.

Production

Same as gr4_mlp production.

Exchange

Same as gr4_mlp exchange.

Transfer

Same as grc transfer except the equations of splitting the production runoff and percolation \(p_r+p_{erc}\)

\begin{eqnarray} &p_{rr}(x, t)& &=& &(0.6 - 0.4 f_{c2}) (0.9 - 0.9 f_{c1}^2) (p_r(x, t) + p_{erc}(x, t)) + l_{exc}(x, t)\\ &p_{rl}(x, t)& &=& &(0.4 + 0.4 f_{c2}) (0.9 - 0.9 f_{c1}^2) (p_r(x, t) + p_{erc}(x, t))\\ &p_{rd}(x, t)& &=& &(0.1 + 0.9 f_{c1}^2) (p_r(x, t) + p_{erc}(x, t)) \end{eqnarray}

grd_mlp

This hydrological module is principally based on the grd operators, with the integration of a neural network for correcting internal water fluxes as follows:

Interception

Same as grd interception.

Process-parameterization neural network

\[[f_p, f_e](x,t) = \phi\left([p_n, e_n](x,t), [\tilde{h_p}, \tilde{h_t}](x,t-1);\boldsymbol{\rho}\right)\]

where \(p_n, e_n\) are the neutralized precipitation and potential evapotranspiration obtained from interception; \(\tilde{h_p}, \tilde{h_t}\) are the normalized states of the production and transfer reservoirs; \(f_p, f_e\) are the corrections applied to internal fluxes as follows.

Production

Same as gr4_mlp production.

Transfer

Same as grd transfer.

loieau_mlp

This hydrological module is principally based on the loieau operators, with the integration of a neural network for correcting internal water fluxes as follows:

Interception

Same as grd interception.

Process-parameterization neural network

\[[f_p, f_e, f_c](x,t) = \phi\left([p_n, e_n](x,t), [\tilde{h_a}, \tilde{h_c}](x,t-1);\boldsymbol{\rho}\right)\]

where \(p_n, e_n\) are the neutralized precipitation and potential evapotranspiration obtained from interception; \(\tilde{h_a}, \tilde{h_c}\) are the normalized states of the production and transfer reservoirs; \(f_p, f_e, f_c\) are the corrections applied to internal fluxes as follows.

Production

Same as gr4_mlp production.

Note

The parameter \(c_p\) is replaced by \(c_a\) and the state \(h_p\) by \(h_a\)

Transfer

Same as loieau transfer except the equations of splitting the production runoff and percolation \(p_r+p_{erc}\)

\begin{eqnarray} &p_{rr}(x, t)& &=& &(0.9 - 0.9 f_c^2)(p_r(x, t) + p_{erc}(x, t))\\ &p_{rd}(x, t)& &=& &(0.1 + 0.9 f_c^2)(p_r(x, t) + p_{erc}(x, t)) \end{eqnarray}

Continuous state-space Génie Rural with 4 parameters (gr4_ode)

This continuous state-space representation of the GR4 model is adapted from Santos et al. [2018] for both lumped and distributed models. Instead of relying on an algebraic approach based on an analytical solution, this representation involves numerically solving the ordinary differential equations (ODEs) of the GR4 model:

\[\begin{split}\frac{d\boldsymbol{h}}{dt}=\left(\begin{array}{c} \frac{dh_{p}}{dt}\\ \frac{dh_{t}}{dt} \end{array}\right) = \left( \begin{array}{c} \left(1-\tilde{h_p}^{\alpha_1}\right)p_n-\tilde{h_p}(2-\tilde{h_p})e_n \\ 0.9\tilde{h_p}^{\alpha_1}p_n+k_{exc}\tilde{h_t}^{\alpha_3}- \frac{c_t}{\alpha_2-1}\tilde{h_t}^{\alpha_2} \end{array} \right)\end{split}\]

where \(\alpha_1=2, \alpha_2=5, \alpha_3=3.5\) are classical GR constants (cf. Perrin et al. [2003], Santos et al. [2018]); \(p_n, e_n\) are the neutralized precipitation and potential evapotranspiration obtained from interception; \(\tilde{h_p}, \tilde{h_t}\) are the normalized states of the production and transfer reservoirs.

This ODE system is solved using an implicit Euler scheme, where the Newton-Raphson method is used to approximate the sought states with a Jacobian matrix explicitly computed.

Then, hydrological runoff flux (lateral discharge feeding the routing module) produced at the pixel scale is computed by the closure equation of the ODE system as follows:

\[q_{t} = 0.1\tilde{h_p}^{\alpha_1}p_n + k_{exc}\tilde{h_t}^{\alpha_3} + \frac{c_t}{\alpha_2-1}\tilde{h_t}^{\alpha_2}\]

Hybrid GR4 with neural ODEs (gr4_ode_mlp)

This hybrid continuous state-space model is embedded within an MLP into the ODEs for process-parameterization. This process-parameterization neural network takes as inputs the neutralized precipitation, the neutralized potential evapotranspiration, and the model states from the previous time step, and produces the corrections of internal water fluxes as outputs:

\[[f_p, f_e, f_t, f_l](x,t) = \phi\left([p_n, e_n](x,t), [\tilde{h_p}, \tilde{h_t}](x,t-1);\boldsymbol{\rho}\right)\]

where \(p_n, e_n\) are the neutralized precipitation and potential evapotranspiration obtained from interception; \(\tilde{h_p}, \tilde{h_t}\) are the normalized states of the production and transfer reservoirs; \(f_p, f_e, f_t, f_l\) are the corrections applied to the ODE system as follows.

\[\begin{split}\frac{d\boldsymbol{h}}{dt}=\left(\begin{array}{c} \frac{dh_{p}}{dt}\\ \frac{dh_{t}}{dt} \end{array}\right) = \left( \begin{array}{c} \left(1-\tilde{h_p}^{\alpha_1}\right)p_n(1+f_p)-\tilde{h_p}(2-\tilde{h_p})e_n(1+f_e) \\ 0.9\tilde{h_p}^{\alpha_1}p_n(1+f_p)+k_{exc}\tilde{h_t}^{\alpha_3}(1+f_l)- \frac{c_t}{\alpha_2-1}\tilde{h_t}^{\alpha_2}(1+f_t) \end{array} \right)\end{split}\]

where \(\alpha_1=2, \alpha_2=5, \alpha_3=3.5\) are classical GR constants (cf. Perrin et al. [2003], Santos et al. [2018]).

Note

The output layer of this neural network uses a TanH activation function to map the hydrological flux corrections to the range \(]-1, 1[\). The hidden layer(s) use a SiLU function, which is twice differentiable everywhere and provides smooth gradients. This is essential because the process-parameterization network must be twice differentiable—once for solving the ODEs and once for the calibration process to ensure numerical consistency during optimization—particularly as we aim to preserve the original structure by producing outputs close to zero at the beginning of optimization.

This ODE system is solved using an implicit Euler scheme, where the Newton-Raphson method is used to approximate the sought states with a Jacobian matrix explicitly computed. The Jacobian matrix is computed using the chain rule, where the derivatives of the neural network are computed using the backpropagation algorithm.

Then, hydrological runoff flux (lateral discharge feeding the routing module) produced at the pixel scale is computed by the closure equation of the ODE system as follows:

\[q_{t} = 0.1\tilde{h_p}^{\alpha_1}p_n(1+f_p) + k_{exc}\tilde{h_t}^{\alpha_3}(1+f_l) + \frac{c_t}{\alpha_2-1}\tilde{h_t}^{\alpha_2}(1+f_t)\]

Génie Rural with imperviousness

This imperviousness feature allows for the calculation of the impervious proportion of a pixel’s surface and takes this into account when computing infiltration and evapotranspiration fluxes applied to the GR type production reservoir. The imperviousness coefficients \(imperv(x)\) influence the fluxes of the production reservoir of each cell by being applied to the neutralized rainfall \(p_n(x,t)\) and the evapotranspiration \(e_s(x,t)\). The imperviousness coefficients must range between 0 and 1 and be specified through an input map that is consistent with the model grid. This map can be obtained, for example, from soil occupation processing. For instance, if the imperviousness coefficient is close to 1, the production part receives less neutralized rainfall \(p_n\) and there is less evapotranspiration \(e_s\) from the impermeable soil. This imperviousness accounting for the GR reservoir is applicable to GR model structures in smash. This is illustrated here on the GR4 structure.

Diagram of the gr4 hydrological operator with imperviousness, a simplified GR like model for spatialized modeling.

Production

• Compute the neutralized precipitation \(p_n\) on impermeable soil

\begin{eqnarray} &p_n(x, t)& &=& & \left(1 - imperv(x)\right)\ p_n(x, t) \end{eqnarray}

• Compute the production infiltrating precipitation \(p_s\) and evapotranspiration \(e_s\)

\begin{eqnarray} &p_s(x, t)& &=& &c_p(x) (1 - \tilde{h_p}(x, t - 1)^2) \frac{\tanh\left(\frac{p_n(x, t)}{c_p(x)}\right)}{1 + \tilde{h_p}(x, t - 1) \tanh\left(\frac{p_n(x, t)}{c_p(x)}\right)}\\ &e_s(x, t)& &=& &(1 - imperv(x)) \left(\tilde{h_p}(x, t - 1) c_p(x) (2 - \tilde{h_p}(x, t - 1)) \frac{\tanh\left(\frac{e_n(x, t)}{c_p(x)}\right)}{1 + (1 - \tilde{h_p}(x, t - 1)) \tanh\left(\frac{e_n(x, t)}{c_p(x)}\right)} \right) \end{eqnarray}

Variable Infiltration Curve 3 Layers (vic3l)

This hydrological operator is derived from the VIC model [Liang et al., 1994].

Hint

Helpful links about VIC:

• Model overview

• References

• GitHub

Diagram of the vic3l like hydrological operator

It can be expressed as follows:

\[q_{t}(x, t) = f\left(\left[P, E\right](x, t), m_{lt}(x, t), \left[b, c_{usl}, c_{msl}, c_{bsl}, k_s, p_{bc}, d_{sm}, d_s, w_s\right](x), \left[h_{cl}, h_{usl}, h_{msl}, h_{bsl}\right](x, t)\right)\]

with \(q_{t}\) the elemental discharge, \(P\) the precipitation, \(E\) the potential evapotranspiration, \(m_{lt}\) the melt flux from the snow operator, \(b\) the variable infiltration curve parameter, \(c_{usl}\) the maximum capacity of the upper soil layer, \(c_{msl}\) the maximum capacity of the medium soil layer, \(c_{bsl}\) the maximum capacity of the bottom soil layer, \(k_s\) the saturated hydraulic conductivity, \(p_{bc}\) the Brooks and Corey exponent, \(d_{sm}\) the maximum velocity of baseflow, \(d_s\) the non-linear baseflow threshold maximum velocity, \(w_s\) the non-linear baseflow threshold soil moisture, \(h_{cl}\) the state of the canopy layer, \(h_{usl}\) the state of the upper soil layer, \(h_{msl}\) the state of the medium soil layer and \(h_{bsl}\) the state of the bottom soil layer.

Note

Linking with the forward problem equation (1)

• Internal fluxes: \(\{q_{t}, m_{lt}\}\in\boldsymbol{q}\)

• Atmospheric forcings: \(\{P, E\}\in\boldsymbol{\mathcal{I}}\)

• Parameters: \(\{b, c_{usl}, c_{msl}, c_{bsl}, k_s, p_{bc}, d_{sm}, d_s, w_s\}\in\boldsymbol{\theta}\)

• Normalized states: \(\{\tilde{h_{cl}}, \tilde{h_{usl}}, \tilde{h_{msl}}, \tilde{h_{bsl}}\}\), where \(\tilde{h_{cl}} = \frac{h_{cl}}{c_{usl}}\), \(\tilde{h_{usl}} = \frac{h_{usl}}{c_{usl}}\), \(\tilde{h_{msl}} = \frac{h_{msl}}{c_{msl}}\), and \(\tilde{h_{bsl}} = \frac{h_{bsl}}{c_{bsl}}\), with states \(\{h_{cl}, h_{usl}, h_{msl}, h_{bsl}\} \in \boldsymbol{h}\)

The function \(f\) is resolved numerically as follows:

Canopy layer interception

• Compute the canopy layer interception evapotranspiration \(e_c\)

\[e_c(x, t) = \min(E(x, t)\tilde{h_{cl}}(x, t - 1)^{2/3}, P(x, t) + m_{lt}(x, t) + \tilde{h_{cl}}(x, t - 1))\]

• Compute the neutralized precipitation \(p_n\) and evapotranspiration \(e_n\)

\begin{eqnarray} &p_n(x, t)& &=& &\max\left(0, P(x, t) + m_{lt}(x, t) - (1 - \tilde{h_{cl}}(x, t - 1)) - e_c(x, t)\right)\\ &e_n(x, t)& &=& &E(x, t) - e_c(x, t) \end{eqnarray}

• Update the normalized canopy layer interception state \(\tilde{h_{cl}}\)

\[\tilde{h_{cl}}(x, t) = \tilde{h_{cl}}(x, t - 1) + P(x, t) - e_c(x, t) - p_n(x, t)\]

Upper soil layer evapotranspiration

• Compute the maximum \(i_{m}\) and the corresponding soil saturation \(i_{0}\) infiltration

\begin{eqnarray} &i_{m}(x, t)& &=& &(1 + b(x))c_{usl}(x)\\ &i_{0}(x, t)& &=& &i_{m}(x, t)\left(1 - (1 - \tilde{h_{usl}}(x, t - 1))^{1/(1 - b(x))}\right) \end{eqnarray}

• Compute the upper soil layer evapotranspiration \(e_s\)

\begin{eqnarray} e_s(x, t) = \begin{cases} e_n(x, t) &\text{if} \; i_{0}(x, t) \geq i_{m}(x, t) \\ \beta(x, t)e_n(x, t) &\text{otherwise} \end{cases} \end{eqnarray}

with \(\beta\), the beta function in the ARNO evapotranspiration [Todini, 1996] (Appendix A)

• Update the normalized upper soil layer reservoir state \(\tilde{h_{usl}}\)

\[\tilde{h_{usl}}(x, t) = \tilde{h_{usl}}(x, t - 1) - \frac{e_s(x, t)}{c_{usl}(x)}\]

Infiltration

• Compute the maximum capacity \(c_{umsl}\), the soil moisture \(w_{umsl}\) and the relative state \(h_{umsl}\) of the first two layers

\begin{eqnarray} &c_{umsl}(x)& &=& &c_{usl}(x) + c_{msl}(x)\\ &w_{umsl}(x, t - 1)& &=& &\tilde{h_{usl}}(x, t - 1)c_{usl}(x) + \tilde{h_{msl}}(x, t - 1)c_{msl}(x)\\ &h_{umsl}(x, t - 1)& &=& &\frac{w_{umsl}(x, t - 1)}{c_{umsl}(x)} \end{eqnarray}

• Compute the maximum \(i_{m}\) and the corresponding soil saturation \(i_{0}\) infiltration

\begin{eqnarray} &i_{m}(x, t)& &=& &(1 + b(x))c_{umsl}(x)\\ &i_{0}(x, t)& &=& &i_{m}(x, t)\left(1 - (1 - h_{umsl}(x, t - 1))^{1/(1 - b(x))}\right) \end{eqnarray}

• Compute the infiltration \(i\)

\begin{eqnarray} i(x, t) = \begin{cases} c_{umsl}(x) - w_{umsl}(x, t - 1) &\text{if} \; i_{0}(x, t) + p_n(x, t) > i_{m}(x, t) \\ c_{umsl}(x) - w_{umsl}(x, t - 1) - c_{umsl}(x)\left(1 - \frac{i_{0}(x, t) + p_n(x, t)}{i_m(x, t)}\right)^{b(x) + 1} &\text{otherwise} \end{cases} \end{eqnarray}

• Distribute the infiltration \(i\) between the first two layers, \(i_{usl}\) and \(i_{msl}\)

\begin{eqnarray} &i_{usl}(x, t)& &=& &\min((1 - \tilde{h_{usl}}(x, t - 1)c_{usl}(x), i(x, t))\\ &i_{msl}(x, t)& &=& &\min((1 - \tilde{h_{msl}}(x, t - 1)c_{msl}(x), i(x, t) - i_{usl}(x, t)) \end{eqnarray}

• Update the first two layers reservoir states normalized, \(\tilde{h_{usl}}\) and \(\tilde{h_{msl}}\)

\begin{eqnarray} &\tilde{h_{usl}}(x, t)& &=& &\tilde{h_{usl}}(x, t - 1) + i_{usl}(x, t)\\ &\tilde{h_{msl}}(x, t)& &=& &\tilde{h_{msl}}(x, t - 1) + i_{msl}(x, t) \end{eqnarray}

• Compute the runoff \(q_r\)

\[q_r(x, t) = p_n(x, t) - (i_{usl}(x, t) + i_{msl}(x, t))\]

Drainage

• Compute the soil moisture in the first two layers, \(w_{usl}\) and \(w_{msl}\)

\begin{eqnarray} &w_{usl}(x, t - 1)& &=& &\tilde{h_{usl}}(x, t - 1)c_{usl}(x)\\ &w_{msl}(x, t - 1)& &=& &\tilde{h_{msl}}(x, t - 1)c_{msl}(x) \end{eqnarray}

• Compute the drainage flux \(d_{umsl}\) from the upper soil layer to medium soil layer

\[d_{umsl}(x, t^*) = k_s(x) * \tilde{h_{usl}}(x, t - 1)^{p_{bc}}\]

• Update the drainage flux \(d_{umsl}\) according to under and over soil layer saturation

\[d_{umsl}(x, t) = \min(d_{umsl}(x, t^*), \min(w_{usl}(x, t - 1), c_{msl}(x) - w_{msl}(x, t - 1)))\]

• Update the first two layers reservoir states normalized, \(\tilde{h_{usl}}\) and \(\tilde{h_{msl}}\)

\begin{eqnarray} &\tilde{h_{usl}}(x, t)& &=& &\tilde{h_{usl}}(x, t - 1) - \frac{d_{umsl}(x, t)}{c_{usl}(x)}\\ &\tilde{h_{msl}}(x, t)& &=& &\tilde{h_{msl}}(x, t - 1) + \frac{d_{umsl}(x, t)}{c_{msl}(x)} \end{eqnarray}

Note

The same approach is performed for drainage in the medium and bottom layers. Hence the three first steps are skiped for readability and the update of the reservoir states is directly written.

• Update of the normalized reservoirs states, \(\tilde{h_{msl}}\) and \(\tilde{h_{bsl}}\)

\begin{eqnarray} &\tilde{h_{msl}}(x, t)& &=& &\tilde{h_{msl}}(x, t - 1) - \frac{d_{mbsl}(x, t)}{c_{msl}(x)}\\ &\tilde{h_{bsl}}(x, t)& &=& &\tilde{h_{bsl}}(x, t - 1) + \frac{d_{mbsl}(x, t)}{c_{bsl}(x)} \end{eqnarray}

Baseflow

• Compute the baseflow \(q_b\)

\begin{eqnarray} q_b(x, t) = \begin{cases} \frac{d_{sm}(x)d_s(x)}{w_s(x)}\tilde{h_{bsl}}(x, t - 1) &\text{if} \; \tilde{h_{bsl}}(x, t - 1) > w_s(x) \\ \frac{d_{sm}(x)d_s(x)}{w_s(x)}\tilde{h_{bsl}}(x, t - 1) + d_{sm}(x)\left(1 - \frac{d_s(x)}{w_s(x)}\right)\left(\frac{\tilde{h_{bsl}}(x, t - 1) - w_s(x)}{1 - w_s(x)}\right)^2 &\text{otherwise} \end{cases} \end{eqnarray}

• Update the normalized bottom soil layer reservoir state \(\tilde{h_{bsl}}\)

\[\tilde{h_{bsl}}(x, t) = \tilde{h_{bsl}}(x, t - 1) - \frac{q_b(x, t)}{c_{bsl}(x)}\]

Routing operator \(\mathcal{M}_{hy}\)

The following routing operators are grid-based and adapted to perform on the same grid as the snow and production operators. They take as input an 8-direction (D8) drainage plan \(\mathcal{D}_{\Omega}\left(x\right)\) obtained through terrain elevation processing.

For all the following models, the 2D flow routing problem over the spatial domain \(\Omega\) reduces to a 1D problem by using the drainage plan \(\mathcal{D}_{\Omega}\left(x\right)\). The latest, for a given cell \(x\in\Omega\) defines 1 to 7 upstream cells which surface discharge can inflow the current cell \(x\) - each cell has a unique downstream cell.

Instantaneous Routing (lag0)

This routing operator is a simple aggregation of upstream discharge to downstream following the drainage plan. It can be expressed as follows:

\[Q(x, t) = f\left(Q(x', t), q_{t}(x, t)\right),\;\forall x'\in \Omega_x\]

with \(Q\) the surface discharge, \(q_t\) the elemental discharge and \(\Omega_x\) a 2D spatial domain that corresponds to all upstream cells flowing into cell \(x\), i.e. the whole upstream catchment. Note that \(\Omega_x\) is a subset of \(\Omega\), \(\Omega_x\subset\Omega\) and for the most upstream cells, \(\Omega_x=\emptyset\).

Note

Linking with the forward problem equation (1)

• Surface discharge: \(Q\)

• Internal fluxes: \(\{q_{t}\}\in\boldsymbol{q}\)

The function \(f\) is resolved numerically as follows:

Upstream discharge

• Compute the upstream discharge \(q_{up}\)

\begin{eqnarray} q_{up}(x, t) = \begin{cases} 0 &\text{if} \; \Omega_x = \emptyset \\ \sum_{k\in\Omega_x} Q(k, t) &\text{otherwise} \end{cases} \end{eqnarray}

Surface discharge

• Compute the surface discharge \(Q\)

\[Q(x, t) = q_{up}(x, t) + \alpha(x) q_t(x, t)\]

with \(\alpha\) a conversion factor from \(mm.\Delta t^{-1}\) to \(m^3.s^{-1}\) for a single cell.

Linear Reservoir (lr)

This routing operator is using a linear reservoir to rout upstream discharge to downstream following the drainage plan. It can be expressed as follows:

\[Q(x, t) = f\left(Q(x', t), q_{t}(x, t), l_{lr}(x), h_{lr}(x, t)\right),\;\forall x'\in \Omega_x\]

with \(Q\) the surface discharge, \(q_t\) the elemental discharge, \(l_{lr}\) the routing lag time, \(h_{lr}\) the state of the routing reservoir and \(\Omega_x\) a 2D spatial domain that corresponds to all upstream cells flowing into cell \(x\). Note that \(\Omega_x\) is a subset of \(\Omega\), \(\Omega_x\subset\Omega\) and for the most upstream cells, \(\Omega_x=\emptyset\).

Note

Linking with the forward problem equation (1)

• Surface discharge: \(Q\)

• Internal fluxes: \(\{q_{t}\}\in\boldsymbol{q}\)

• Parameters: \(\{l_{lr}\}\in\boldsymbol{\theta}\)

• States: \(\{h_{lr}\}\in\boldsymbol{h}\)

The function \(f\) is resolved numerically as follows:

Upstream discharge

Same as lag0 upstream discharge, see LAG0 Upstream Discharge.

Surface discharge

• Update the routing reservoir state \(h_{lr}\)

\[h_{lr}(x, t^*) = h_{lr}(x, t) + \frac{1}{\beta(x)} q_{up}(x, t)\]

with \(\beta\) a conversion factor from \(mm.\Delta t^{-1}\) to \(m^3.s^{-1}\) for the whole upstream domain \(\Omega_x\).

• Compute the routed discharge \(q_{rt}\)

\[q_{rt}(x, t) = h_{lr}(x, t^*) \left(1 - \exp\left(\frac{-\Delta t}{60\times l_{lr}}\right)\right)\]

• Update the routing reservoir state \(h_{lr}\)

\[h_{lr}(x, t) = h_{lr}(x, t^*) - q_{rt}(x, t)\]

• Compute the surface discharge \(Q\)

\[Q(x, t) = \beta(x)q_{rt}(x, t) + \alpha(x)q_t(x, t)\]

with \(\alpha\) a conversion factor from from \(mm.\Delta t^{-1}\) to \(m^3.s^{-1}\) for a single cell.

Kinematic Wave (kw)

This routing operator is based on a conceptual 1D kinematic wave model that is numerically solved with a linearized implicit numerical scheme [Chow et al., 1998]. This is applicable given the drainage plan \(\mathcal{D}_{\Omega}\left(x\right)\) that enables reducing the routing problem to 1D.

The kinematic wave model is a simplification of 1D Saint-Venant hydraulic model. First the mass equation writes:

(1)\[\partial_{t}A+\partial_{x}Q =q\]

with \(\partial_{\square}\) denoting the partial derivation either in time or space, \(A\) the cross sectional flow area, \(Q\) the flow discharge and \(q\) the lateral inflows.

Assuming that the momentum equation reduces to

(2)\[S_0=S_f\]

with \(S_0\) the bottom slope and \(S_f\) the friction slope - i.e. a locally uniform flow with energy grade line parallel to the channel bottom. This momentum equation can be expressed in the following form, as described by Chow et al. [1998]

(3)\[A=a_{kw} Q ^{b_{kw}}\]

with \(a_{kw}\) and \(b_{kw}\) two constants to be estimated - that can also be written using Manning friction law.

Injecting the momentum parameterization of Eq. 3 into mass equation Eq. 1 leads to the following one equation kinematic wave model [Chow et al., 1998]:

(4)\[\partial_{x}Q+a_{kw}b_{kw} Q^{b_{kw}-1}\partial_{t}Q=q\]

Hint

Helpful link about kinematic wave:

• Numerical Solution (page 294, section 9.6)

The solution of this equation can written as:

\[Q(x, t) = f\left(Q(x', t'), q_{t}(x, t'), \left[a_{kw}, b_{kw}\right](x)\right),\;\forall (x', t') \in \Omega_x\times[t-1, t]\]

with \(Q\) the surface discharge, \(q_t\) the elemental discharge, \(a_{kw}\) the alpha kinematic wave parameter, \(b_{kw}\) the beta kinematic wave parameter and \(\Omega_x\) a 2D spatial domain that corresponds to all upstream cells flowing into cell \(x\). Note that \(\Omega_x\) is a subset of \(\Omega\), \(\Omega_x\subset\Omega\) and for the most upstream cells, \(\Omega_x=\emptyset\).

Note

Linking with the forward problem equation (1)

• Surface discharge: \(Q\)

• Internal fluxes: \(\{q_{t}\}\in\boldsymbol{q}\)

• Parameters: \(\{a_{kw}, b_{kw}\}\in\boldsymbol{\theta}\)

For the sake of clarity, the following variables are renamed for this section and the finite difference numerical scheme writing:

Renamed variables

Before	After
\(Q(x, t)\)	\(Q_i^j\)
\(Q(x, t - 1)\)	\(Q_{i}^{j-1}\)
\(q_t(x, t)\)	\(q_{i}^{j}\)
\(q_t(x, t - 1)\)	\(q_{i}^{j-1}\)

The function \(f\) is resolved numerically as follows:

Upstream discharge

Same as lag0 upstream discharge, see LAG0 Upstream Discharge.

Note

\(q_{up}\) is denoted here \(Q_{i-1}^{j}\)

Surface discharge

• Compute the intermediate variables \(d_1\) and \(d_2\)

\begin{eqnarray} &d_1& &=& &\frac{\Delta t}{\Delta x}\\ &d_2& &=& &a_{kw} b_{kw} \left(\frac{\left(Q_i^{j-1} + Q_{i-1}^j\right)}{2}\right)^{b_{kw} - 1} \end{eqnarray}

• Compute the intermediate variables \(n_1\), \(n_2\) and \(n_3\)

\begin{eqnarray} &n_1& &=& &d_1 Q_{i-1}^j\\ &n_2& &=& &d_2 Q_{i}^{j-1}\\ &n_3& &=& &d_1 \frac{\left(q_i^{j-1} + q_{i}^{j}\right)}{2} \end{eqnarray}

• Compute the surface discharge \(Q_i^j\)

\[Q_i^j = Q(x, t) = \frac{n_1 + n_2 + n_3}{d_1 + d_2}\]