Hydrological Signatures#
This section provides a detailed explanation of how to compute and visualize various hydrological signatures, which are described in the Math / Num Documentation section.
First, open a Python interface:
python3
Imports#
We will first import the necessary libraries for this tutorial.
In [1]: import smash
In [2]: import pandas as pd
In [3]: import matplotlib.pyplot as plt
Model object creation#
Now, we need to create a smash.Model object.
For this case, we will use the Cance dataset as an example.
Load the setup and mesh dictionaries using the smash.factory.load_dataset function and create the smash.Model object.
In [4]: setup, mesh = smash.factory.load_dataset("Cance")
In [5]: model = smash.Model(setup, mesh)
</> Computing mean atmospheric data
</> Adjusting GR interception capacity
Signatures computation#
We can compute the observed signatures as follows. By default, all signatures are computed, but we choose several of them.
For example, here we choose to compute the continuous runoff coefficient ('Crc'), the flow percentile at 90% ('Cfp90'),
the flood event runoff coefficient ('Erc'), and the peak flow ('Epf').
In [6]: sig_obs = smash.signatures(model, sign=["Crc", "Cfp90", "Erc", "Epf"], domain="obs")
To compute the simulated signatures, a simulation (either forward run or optimization) has to be performed to generate the simulated discharge. We compute the same signatures as the observed ones for the simulated discharge.
In [7]: model.forward_run()
</> Forward Run
In [8]: sig_sim = smash.signatures(model, sign=["Crc", "Cfp90", "Erc", "Epf"], domain="sim")
The signatures computation result object contains two attributes which are two different dictionaries:
cont: Continuous signatures computation result,event: Flood event signatures computation result.
In [9]: sig_sim.cont
Out[9]:
code Crc Cfp90
0 V3524010 0.208410 27.806807
1 V3515010 0.139829 5.161739
2 V3517010 0.139431 1.355470
In [10]: sig_sim.event
Out[10]:
code season ... Erc Epf
0 V3524010 autumn ... 0.322406 100.448669
1 V3515010 autumn ... 0.211647 20.168100
2 V3517010 autumn ... 0.219968 5.356512
[3 rows x 7 columns]
For flood event signatures computation, more options can be specified such as the threshold for flood event detection, the maximum duration of the flood event, etc.
The segmentation algorithm used to detect the flood events can be adjusted by setting the event_seg parameter in the smash.signatures function.
This parameter is a dictionary with keys that are the parameters used for the segmentation algorithm (refer to the tutorial on hydrograph segmentation for more details).
For instance, we can reduce the quantile threshold for flood event detection to 0.99.
In [11]: sig_obs_2 = smash.signatures(model, sign=["Erc", "Epf"], domain="obs", event_seg={"peak_quant": 0.99})
In [12]: sig_obs_2.event
Out[12]:
code season ... Erc Epf
0 V3524010 autumn ... 0.566425 229.444000
1 V3524010 autumn ... 0.595655 317.380005
2 V3515010 autumn ... 0.459372 41.492001
3 V3515010 autumn ... 0.538027 49.358002
4 V3517010 autumn ... 0.403944 9.548000
5 V3517010 autumn ... 0.550013 14.939000
[6 rows x 7 columns]
In [13]: sig_sim_2 = smash.signatures(model, sign=["Erc", "Epf"], domain="sim", event_seg={"peak_quant": 0.99})
In [14]: sig_sim_2.event
Out[14]:
code season ... Erc Epf
0 V3524010 autumn ... 0.070561 81.095398
1 V3524010 autumn ... 0.322406 100.448669
2 V3515010 autumn ... 0.040480 15.753152
3 V3515010 autumn ... 0.211647 20.168100
4 V3517010 autumn ... 0.031992 5.131624
5 V3517010 autumn ... 0.219968 5.356512
[6 rows x 7 columns]
Signatures visualization#
Now, we visualize, for instance, the simulated and observed peak flow in the boxplot below.
In [15]: df_obs = sig_obs_2.event
In [16]: df_sim = sig_sim_2.event
In [17]: df = pd.concat([df_obs.assign(domain="Observed"), df_sim.assign(domain="Simulated")], ignore_index=True)
In [18]: boxplot = df.boxplot(column=["Epf"], by="domain")

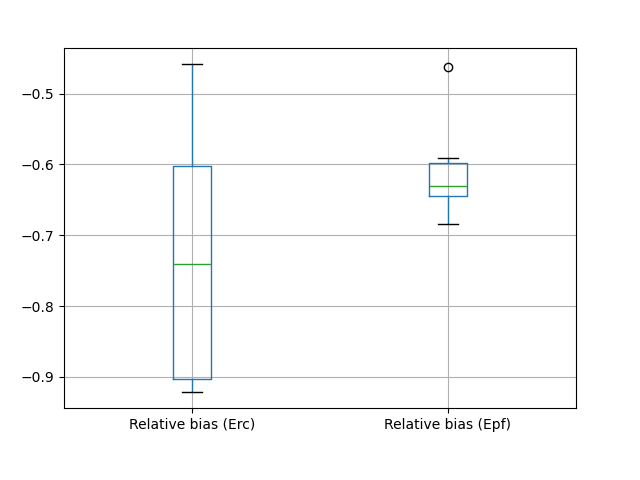
We can also compute the relative bias for any desired signature. For example, the computation and visualization of the relative bias for the two selected flood event signatures are shown below.
In [19]: ERR_Erc = sig_sim_2.event["Erc"] / sig_obs_2.event["Erc"] - 1
In [20]: ERR_Epf = sig_sim_2.event["Epf"] / sig_obs_2.event["Epf"] - 1
In [21]: df_err = pd.DataFrame({"Relative bias (Erc)": ERR_Erc, "Relative bias (Epf)": ERR_Epf})
In [22]: boxplot_err = df_err.boxplot()